Collective Wisdom: Lessons from the Theory of Judgment Aggregation

Christian List discusses the lessons we can learn about collective wisdom by combining insights from the emerging theory of judgment aggregation with insights from Condorcet’s jury theorem. This paper is part of an issue on Collective wisdom.

1. Introduction

Can collectives be wise¹The aim of this paper is to review the lessons about collective wisdom that can be learnt from recent work on the theory of judgment aggregation. The paper draws significantly on earlier work of mine in List (2005; 2008). Some of the ideas discussed here also draw on joint work with Philip Pettit on group agency in List and Pettit (forthcoming); chapters 2 and 4 of our forthcoming book, in particular, develop some related issues in greater detail. I wish to record my debt to Philip Pettit as well as to my other regular co-author, Franz Dietrich, who has also significantly influenced my thinking on the present themes. I am very grateful to Karen Croxson, Jon Elster, Hélène Landemore and the other participants in the Colloquium on Collective Wisdom at the Collège de France, May 2008, for helpful comments and discussion.? The thesis that they can has recently received a lot of attention. It has been argued that, in many judgmental or decision-making tasks, suitably organized groups can outperform their individual members. In particular, it has been suggested that groups are good at meeting what I call the correspondence challenge (as in correspondence with the facts): By pooling information that is dispersed among the individual members, a group can arrive at judgments that accurately track some independent truths or make decisions that maximize an independent objective function (for a popular discussion, see Surowiecki 2004).

One of the best-known illustrations of this effect is given by Condorcet’s jury theorem: If each member of a jury has an equal and independent chance better than random, but worse than perfect, of making a correct judgment on whether a defendant is guilty, the majority of jurors is more likely to be correct on the matter of guilt than each individual juror, and the probability of a correct majority judgment approaches certainty as the jury size increases (e.g., Grofman, Owen et al. 1983). Many generalizations and extensions of this result have been obtained, and a lot can be said about the conditions under which information pooling is truth-conducive and those under which it isn’t (see, among many others, Boland 1989; Estlund 1994; List and Goodin 2001).

While the ability to make judgments that correspond with the facts is clearly an important dimension along which a group’s claim to wisdom can be assessed, it is not the only one. The group’s ability to come up with a coherent body of judgments also matters; let me call this the coherence challenge. A necessary condition for wisdom, it seems, is that one is able to organize one’s judgments in a coherent manner. Minimally, this requires forming a body of judgments that is free from inconsistencies – or at least free from blatant inconsistencies. More strongly, it may require forming a body of judgments that satisfies certain closure conditions, for instance closure under logical consequence. Expert panels or multi-member courts, for example, would hardly be regarded as wise if they were unable to deliver judgments that are at least minimally coherent. Even a good factual accuracy of some of their judgments would not seem to be enough to compensate for certain violations of coherence. Correspondence and coherence both matter²Inspired by a discussion with Goldman (2004), I have previously discussed these two challenges under the labels ‘rationality challenge’ and ‘knowledge challenge’ (List 2005). The present terminology is inspired by the coherence and correspondence theories of truth or knowledge..

In this paper, I discuss the lessons we can learn about collective wisdom from the emerging theory of judgment aggregation (originally formulated in List and Pettit 2002; 2004), as distinct from the literature on Condorcet’s jury theorem. While the large body of work inspired by Condorcet’s jury theorem has been concerned with how groups can meet the correspondence challenge, much of the recent work on judgment aggregation focuses on their performance with regard to the coherence challenge.³ A detailed review is beyond the scope of this paper, but I would like to mention some key contributions. The interest in the problem of judgment aggregation was originally sparked by the so-called doctrinal paradox in jurisprudence, concerning decision making in collegial courts (Kornhauser and Sager 1986; 1993), which was later generalized beyond the judicial context under the name discursive dilemma (Pettit 2001; List and Pettit 2002). The differences between the doctrinal paradox and the discursive dilemma are discussed in a separate note below. List and Pettit (2002) developed a formal model of judgment aggregation, combining Arrovian social choice theory (Arrow 1951/1963) and propositional logic, and proved a first impossibility theorem. Following this original theorem, stronger or refined impossibility results were proved, for example, by Pauly and van Hees (2006), Dietrich (2006) and Dietrich and List (2007a). Moreover, necessary and sufficient conditions on the agenda of propositions leading to such impossibility results were identified by Nehring and Puppe (2002/2007), Dokow and Holzman (forthcoming), Dietrich (2007) and Dietrich and List (2007a). Some of these results have precursors in abstract aggregation theory (Wilson 1975; Rubinstein and Fishburn 1986; Nehring and Puppe 2002). An even earlier precursor is Guilbaud’s (1966) discussion of theories of the general interest. Although much work has focused on proving impossibility results, the literature also contains a number of possibility results (for example, List 2003; 2004; Dietrich 2006; Pigozzi 2006; Dietrich and List 2007c; Dietrich forthcoming). For informal surveys, see List (2006b; forthcoming); for a more formal survey, see List and Puppe (forthcoming). The precise relationship between judgment aggregation and Arrovian preference aggregation is discussed in (List and Pettit 2004) and (Dietrich and List 2007a). Furthermore, while the jury theorem and its extensions are usually taken to support a largely optimistic picture of collective wisdom, the literature on judgment aggregation is now so replete with negative results that it may give the impression that collective wisdom is impossible to attain. As with many pairs of opposite extremes, the truth lies somewhere in the middle, and my suggestion is that insights from both the work on judgment aggregation and the work on Condorcet’s jury theorem are needed to provide a nuanced assessment of a group’s capacity to attain wisdom.

2. Conceptual preliminaries

When does it make sense to describe an entity as wise? Obviously, we wouldn’t describe rocks, sofas or power drills as wise. Human beings, by contrast, are paradigmatically capable of wisdom. Might the concept of wisdom also apply to non-human animals, or to robots? There seems to be no conceptual barrier in describing a complex computational system such as HAL 9000 in Arthur C. Clarke’s Space Odyssey as wise. Similarly, an intelligent and experienced non-human animal such as a primate who plays an important role in the social organization of his or her group may well qualify as wise. What makes the concept of wisdom in principle applicable in all these cases is the fact that the entities in question are agents.⁴ The notion of agency employed here is developed in List and Pettit (forthcoming, chapter 1). It is inspired by Dennett (1987) and Pettit (1993). Human beings, non-human animals and sophisticated robots, unlike rocks, sofas or power drills, can all be understood as having cognitive and emotive states – which encode beliefs and desires, respectively – and as acting systematically on the basis of these states.

While wisdom is usually taken to be a property of agents, I shall here interpret wisdom more weakly as a property of entities that are at least proto-agents, defined as entities with cognitive states, which encode beliefs or judgments. In particular, I use the concept of wisdom to refer to a proto-agent’s capacity to meet the correspondence and coherence challenges defined above. This thin, pragmatic interpretation of wisdom contrasts with thicker, more demanding interpretations which require richer capacities of agency. Solomonic wisdom, for example, clearly goes beyond an agent’s performance at truth-tracking and forming coherent judgments, but I shall set aside these more demanding issues here.

In order to assess the wisdom of collectives in the present, deflationary sense, we must therefore begin by asking whether groups can count as proto-agents. The answer depends on how a given group is organized. A well-organized expert panel, a group of scientific collaborators or the monetary policy committee of a central bank, for example, may well be candidates for proto-agents – perhaps even candidates for fully-fledged agents (following the account of group agency in List and Pettit forthcoming) – whereas a random crowd of pedestrians in the town centre is not; it lacks the required level of integration. In particular, the group must have the capacity to form collective beliefs or judgments, and for this it requires an organizational structure for generating them. This may take the form of a voting procedure, a deliberation protocol, or any other mechanism by which the group can make joint declarations or deliver a joint report. Such procedures are in operation in expert panels, multi-member courts, policy advisory committees and groups of scientific collaborators.

I will follow the literatures on judgment aggregation and on Condorcet’s jury theorem in focusing on the formation of binary ‘acceptance/rejection’ judgments, as opposed to non-binary degrees of beliefs. Specifically, I will assume that a group seeks to form collective ‘acceptance/rejection’ judgments on a given set of propositions and their negations – called the agenda – on the basis of the group members’ individual judgments on them.

Although the case of non-binary beliefs, which typically take the form of subjective probability assignments to propositions, is also important (e.g., Lehrer and Wagner 1981; Genest and Zidek 1986; Dietrich and List 2007d), many real-world judgmental or decision-making tasks by groups or committees require the determinate acceptance or rejection of certain propositions – say, on the guilt of a defendant or the viability of some policy – and this gives particular significance to the binary case.

The propositions on the agenda are formulated in propositional logic, which can express atomic propositions without logical connectives, such as ‘p’, ‘q’, ‘r’ and so on, and compound propositions with logical connectives, such as ‘p and q’, ‘p or q’, ‘if p then q’ and so on.⁵ For an extension of the model to more general logics, see Dietrich (2007). In a simple example, the agenda might contain just a single proposition and its negation, such as ‘the defendant is guilty’ versus ‘the defendant is not guilty’, but below I will consider more complex cases.

The group’s organizational structure will now be modelled as an aggregation procedure. As illustrated in Table 1, an aggregation procedure is a function which assigns to each combination of the group members’ individual ‘acceptance/rejection’ judgments on the propositions on the agenda a corresponding set of collective judgments. A simple example is majority voting, whereby a group judges a given proposition to be true whenever a majority of group members does so. Below I discuss several other aggregation procedures.

Table 1: An aggregation procedure

Input (individual beliefs or judgments) –> Aggregation procedure –> Output (collective beliefs or judgments)

Of course, an aggregation procedure captures only part of a group’s organizational structure, and there are also various different ways in which a group might implement such a procedure. Just think of all the different ways in which the group members may reveal their judgments to the procedure. They might do so through explicit voting, which in turn can take a number of forms (for example, open or anonymous), through discussion or through their actions. However, as I will argue below, the question of whether a group deserves to be called wise depends crucially on the nature of its aggregation procedure – as well as on the performance of its individual members.

Thus the task is to investigate what properties a group’s aggregation procedure must have for the group to meet the coherence challenge, and what properties it must have for the group to meet the correspondence challenge. The next two sections are devoted to these questions. By combining insights from the theory of judgment aggregation with insights from the work on Condorcet’s jury theorem, I hope to shed light on the conditions for collective wisdom.

3. Meeting the coherence challenge

Suppose, then, a group seeks to form collective judgments on some agenda of propositions. Can the group ensure the coherence of these judgments? Let me begin with two examples.

To present the first example, consider an expert panel that has to give advice on the health consequences of air pollution in a big city, especially pollution by very small particles. The experts have to make judgments on the following propositions (and their negations):

‘p’: The average particle pollution level exceeds 50 micrograms per cubic meter air.

‘if p then q’: If the average particle pollution level exceeds this amount, then residents have a significantly increased risk of lung disease.

‘q’: Residents have a significantly increased risk of lung disease.

All three propositions are complex factual propositions on which there may be reasonable disagreement between experts. What happens if the panel uses majority voting as its aggregation procedure? Suppose, as an illustration, that the experts’ individual judgments are as shown in Table 2.

Table 2: A majoritarian inconsistency

	‘p’	‘if p then q’	‘q’
Individual 1	True	True	True
Individual 2	True	False	False
Individual 3	False	True	False
Majority	True	True	False

Then a majority of experts judges ‘p’ to be true, a majority judges ‘if p then q’ to be true, and yet a majority judges ‘q’ to be false. The set of propositions accepted by a majority – ‘p’, ‘if p then q’, and ‘not q’ – is incoherent in two senses here. First, it violates consistency, defined as the requirement that it must be possible for the propositions in the set to be simultaneously true. And second, it fails to be deductively closed, where deductive closure is the requirement that, if the set of accepted propositions entails another proposition that is also on the agenda, then that other proposition should be accepted as well. In the present example, although ‘p’ and ‘if p then q’, which are both collectively accepted, logically entail ‘q’, the latter proposition is not accepted. Clearly, the expert panel fails to meet the coherence challenge in this example.

The second example to be presented is a historical one, reported by Elster (2007, pp. 410-411), concerning the debates in the French Constituent Assembly of 1789 on whether the country should introduce a bicameral or a unicameral system.⁶ I am grateful to Jon Elster for drawing my attention to this example. In very simplified terms, the members of the Assembly had to make judgments on three propositions (and their negations):

‘p’: It is desirable to stabilize the regime.

‘q’: Bicameralism (as opposed to unicameralism) will stabilize the regime.

‘r’: It is desirable to introduce bicameralism (as opposed to unicameralism).

The background assumption is that ‘r’ is to be accepted if and only if both ‘p’ and ‘q’ are accepted. As Elster reports, the Assembly was divided into three groups of roughly equal size. The reactionary right wanted to destabilize the regime but thought that bicameralism would stabilize it, and therefore opposed bicameralism. The moderate centrists wanted to stabilize the regime and thought that bicameralism would do so, and therefore supported bicameralism. The radical left, finally, wanted to stabilize the regime but thought that bicameralism would have the opposite effect, and hence opposed bicameralism. Thus the individual judgments were as shown in Table 3.

Table 3: The French Constituent Assembly

	‘p’	‘q’	‘r’
Reactionaries	False	True	False
Moderates	True	True	True
Radicals	True	False	False
Majority	True	True	False

The overall majority judgments in this example – the acceptance of ‘p’ and ‘q’ and the rejection of ‘r’ – are clearly inconsistent relative to the background assumption that ‘r if and only if p and q’. As Elster observes, bicameralism was defeated because the Assembly ultimately voted on proposition ‘r’. However, he also argues that if the Assembly had explicitly voted on each of ‘p’ and ‘q’ and none of the groups had strategically misrepresented their opinions – which he recognizes to be big ifs – then the outcome might have been the opposite one. In any case, the example suggests that the Constituent Assembly failed to meet the coherence challenge.⁷ In Elster’s presentation of the example, the members of the Assembly hold preferences on whether or not to stabilize the regime and on whether or not to introduce bicameralism, while they hold beliefs on whether or not bicameralism will stabilize the regime. Thus he casts the aggregation problem as a mixed preference-belief aggregation problem. In principle, this interpretation can be made consistent with my formalization as well, but to simplify the exposition I have translated the agents’ preferences into judgments of desirability, thus interpreting their attitudes as cognitive rather than emotive ones. Although there are very important differences between single-attitude aggregation problems (such as pure judgment aggregation) and mixed aggregation problems (such as combined preference-belief aggregation), a discussion of these issues is beyond the scope of this paper.

Both examples are instances of the so-called discursive dilemma (Pettit 2001; List and Pettit 2002), which shows that majority voting does not generally secure collective wisdom, understood in terms of coherence. Specifically, the dilemma consists in the fact that simultaneous majority voting on some suitably connected propositions may lead to a logically inconsistent set of judgments.⁸ This generalizes the earlier doctrinal paradox concerning judicial decisions (Kornhauser and Sager 1986; 1993). To illustrate the earlier problem, suppose a multi-member court seeks to make a decision on whether a defendant is liable for breach of contract (the conclusion) on the basis of two jointly necessary and sufficient conditions (the premises): first, there was a valid contract in place, and second, the defendant’s action was such as to breach a contract of this kind. If one judge holds both premises to be true, a second judge holds the first premise but not the second to be true, and a third judge holds the second premise but not the first to be true, then the majority judgments on the two premises seem to support a liable verdict while a majority of judges individually consider the defendant not to be liable. The ‘doctrinal paradox’ consists in the fact that majority voting on the premises (the premise-based or issue-by-issue procedure) may lead to a different outcome than majority voting on the conclusion (the conclusion-based or case-by-case procedure). The discursive dilemma, more generally, consists in the fact that simultaneous majority voting on any set of suitably connected propositions – whether or not they can be partitioned into premises and conclusions – may yield a logically inconsistent set of judgments. To be precise, the problem of majority inconsistency can arise as soon as the agenda of propositions (and their negations) on which judgments are to be made has at least one minimally inconsistent subset of three or more propositions (for a proof, see Dietrich and List 2007b). However, the examples do not undermine the possibility of attaining collective coherence through some other aggregation procedure, distinct from proposition-by-proposition majority voting. (Indeed, the French Constituent Assembly avoided an overt instance of inconsistent majority judgments by not taking explicit votes on all propositions; rather, they voted only on whether or not to introduce bicameralism.) For all we can infer at this point, the problem might be an isolated artefact of majority voting.

3.1 A general impossibility theorem

Let us therefore set aside the specific aggregation procedure of majority voting, and investigate the logical space of possible aggregation procedures more generally. That logically space is truly vast: Even if an ‘acceptance/rejection’ judgment is to be made just on a single proposition – a rather simple agenda – there are 2ⁿ possible combinations of individual judgments in an n-member group to which corresponding collective judgments must be assigned, and thus there are 2²ⁿ logically possible aggregation procedures (List 2006a). This number not only grows exponentially in the group size n, but even for small groups it exceeds the estimated total number of particles in the universe.

Surely, one would expect, there must exist some aggregation procedures in this large logical space that allow a group to meet the coherence challenge. To find these procedures, let us introduce some minimal conditions that an aggregation procedure might be expected to satisfy.

Universality: The aggregation procedure admits as input any possible combination of consistent and complete individual judgments on the propositions on the agenda, where completeness is the requirement that, for each proposition-negation pair on the agenda, either the proposition or its negation is accepted.

Decisiveness: The aggregation procedure generates as output complete judgments on the propositions on the agenda.

Systematicity: The collective judgment on each proposition on the agenda depends only on the individual judgments on it, and the pattern of dependence is the same across propositions.

These conditions are intended to be minimal in the sense that they are satisfied by a whole range of familiar aggregation procedures, including majority voting or even a dictatorship of a single individual. Ideally, we would like a good aggregation procedure to satisfy conditions that go beyond them. But what are the aggregation procedures that satisfy the present three conditions and guarantee consistent collective judgments? Surprisingly, there are only rather degenerate such procedures.

Theorem (Dietrich and List 2007a): If the propositions on the agenda are non-trivially interconnected, an aggregation procedure satisfies universality, decisiveness and systematicity and generates consistent collective judgments only if it is a dictatorship or inverse dictatorship of one individual.⁹ The notion of non-trivial interconnections between the propositions on the agenda can be made precise. In the present theorem, it requires that (i) the agenda has at least one minimally inconsistent subset of three or more propositions, and (ii) it has at least one minimally inconsistent subset with the additional property that, by negating an even number of propositions in it, it becomes consistent. The agenda in the expert-panel example meets both of these conditions. It is easy to verify that a minimally inconsistent subset of the agenda with the properties required in both (i) and (ii) is the set containing the propositions ‘p’, ‘if p then q’ and ‘not q’. The theorem stated here generalizes the original theorem in List and Pettit (2002) and a subsequent result in Pauly and van Hees (2006). Closely related results, stated in ‘abstract aggregation’ frameworks and using slightly different conditions on the agenda and on the aggregation procedure, have been obtained by Nehring and Puppe (2002/2007) and Dokow and Holzman (forthcoming).

Under such an aggregation procedure, the collective judgments are fully determined by a fixed single individual. In short, majority voting is not the only aggregation procedure that runs into problems like the ones in the examples of the expert panel and the French Constituent Assembly above. Any non-dictatorial (and non-inverse-dictatorial) procedure satisfying universality, decisiveness and systematicity does so.

If these three conditions were regarded as indispensable requirements on an aggregation procedure, then one would have to conclude that the wisdom of a group collapses, at best, into the wisdom of some dictatorial group member or chairperson. Collective wisdom would not be possible in any interesting way. This conclusion, however, would be too quick. It is instructive to see what happens if we relax one of the three conditions.

3.2 Relaxing universality

Universality requires the aggregation procedure to admit as input any possible combination of consistent and complete individual judgments on the propositions on the agenda. An aggregation procedure with this property exhibits a certain kind of ‘robustness’: it works not only for special inputs, but for all possible inputs that may be brought to it. But suppose we require the formation of collective judgments only when there is sufficient agreement among the individuals. Then it becomes possible for majority voting to generate consistent group judgments.

Suppose, in particular, that the group members can be aligned from left to right – this may represent their positions on some cognitive or ideological dimension – such that the following pattern holds: for every proposition on the agenda, the individuals accepting the proposition are either all to the left, or all to the right, of those rejecting it. (This pattern is called unidimensional alignment.) It is then guaranteed that majority voting generates consistent collective judgments, assuming that individual judgments are consistent (List 2003; for generalizations, see Dietrich and List 2007c).

To illustrate this result, consider the following example. Suppose a five-member group seeks to form attitudes towards propositions ‘p’, ‘if p then q’, ‘q’ and their negations, as in the expert-panel example above, and suppose the individual judgments are as shown in Table 4. Here the individuals accepting any given proposition are either all to the left, or all to the right, of those rejecting it.

Table 4: Unidimensionally aligned judgments

	Individual 1	Individual 2	Individual 3	Individual 4	Individual 5
‘p’	False	False	False	False	True
‘if p then q’	True	True	True	True	False
‘q’	True	True	False	False	False

What are the resulting majority judgments? It is easy to see that they coincide with the judgments of the median individual on the left-right alignment – here individual 3 – since no proposition can be accepted by a majority without being accepted by the median individual. As long as the median individual holds consistent judgments, then, the majority judgments are guaranteed to be consistent as well. (Notice that this arrangement is by no means dictatorial, since the median individual may differ from case to case.)

In short, if universality is relaxed to the requirement that the aggregation procedure admit as input only those combinations of individual judgments that satisfy a structure condition like the one just illustrated, then majority voting ensures consistent collective judgments while also satisfying decisiveness and systematicity.

Nonetheless, this solution cannot work in general. Even in an idealized expert panel making judgments on factual matters without any conflicts of interests, disagreement may still be profound, and there is no guarantee that individual judgments will neatly fall into any cohesive pattern. Moreover, in situations of significant conflicts of interests such as in the French Constituent Assembly of 1789, the level of cohesion required for consistent majority judgments may not generally be present. A best-case scenario is perhaps the situation in which the formation of group judgments is preceded by a sufficiently intense and effective period of group deliberation. Such deliberation may move individual judgments towards a more cohesive pattern, as hypothesized by theorists of deliberative democracy (Miller 1992; Knight and Johnson 1994; Dryzek and List 2003). Elsewhere I have obtained some empirical evidence in support of an effect of this kind (List, Luskin et al. 2000/2006). Still, in many collectives the empirical fact of pluralism may require the use of an aggregation procedure satisfying universality.

3.3 Relaxing decisiveness

Decisiveness requires the aggregation procedure to generate as output complete judgments on the propositions on the agenda. Suppose a group is willing not to be opinionated on some proposition-negation pairs; it is willing to accept neither the proposition nor its negation. The group may then be able to generate consistent collective judgments in accordance with the other conditions introduced above. It may use a supermajority or unanimity rule, for example, under which any given proposition is accepted if and only if a particular supermajority of group members – say, two thirds, three quarters, or all of them in the case of unanimity rule – does so. If the required supermajority threshold is sufficiently high – in the example above, any threshold above two-thirds would work – this aggregation procedure guarantees consistent collective judgments, while satisfying universality and systematicity (List 2001; Dietrich and List 2007b).¹⁰ Formally, let k be the size of the largest minimally inconsistent subset of the agenda. Then a supermajority above a proportion of (k-1)/k of the individuals must be required for the acceptance of any proposition in order to ensure collective consistency.

Groups with stringent requirements of consensus, such as the UN Security Council or the EU Council of Ministers, often take this approach, with the result that they frequently have to suspend judgment (for a general discussion of supermajoritarian decision making, see Goodin and List 2006). But many collectives cannot afford indecisiveness; they are expected to make up their minds on the propositions brought to them on the agenda. The expert panel giving advice on air pollution may simply be required to come up with firm judgments on all proposition-negation pairs; incompleteness may not be acceptable here.

Moreover, the escape route from the impossibility theorem via relaxing decisiveness becomes even more limited if we understand coherence as requiring not only the consistency of the group judgments but also its deductive closure. It turns out that, if we keep the earlier theorem’s assumption about the agenda, the only aggregation procedures generating consistent and deductively closed collective judgments and satisfying universality as well as systematicity (and which do not overrule individual judgments in the special case of unanimity) are the so-called oligarchic ones (Dietrich and List 2008).¹¹ For closely related results, see also Gärdenfors (2006) and Dokow and Holzman (2006). Under such a procedure, there exists a fixed subset of the individuals – possibly including everyone, possibly singleton, possibly some other subset – such that the group accepts all and only those propositions that are unanimously accepted by the individuals in the given subset. Both unanimity rule and dictatorships are special cases of oligarchic procedures under this definition, with the relevant subset including either all individuals (in the case of unanimity rule) or just one individual (in the case of a dictatorship). Since every individual in the relevant subset can veto the acceptance of any proposition, there is likely to be stalemate, as soon as there is the slightest diversity of opinion among these individuals.

3.4 Relaxing systematicity

The limited appeal of the previous escape routes from the impossibility theorem suggests that we may need to relax systematicity, by treating different propositions differently in the process of forming collective judgments. A group may do so, for example, by designating some propositions as premises and others as conclusions and assigning priority either to the premises or to the conclusions.

If the group assigns priority to the premises, it may use the so-called premise-based procedure, whereby the group first makes a collective judgment on each premise by taking a majority vote on that premise and then derives its collective judgments on the conclusions from these collective judgments on the premises. In the expert-panel example, propositions ‘p’ and ‘if p then q’ might be designated as premises (perhaps on the grounds that they are more fundamental than ‘q’), and proposition ‘q’ might be designated as a conclusion. The panel might then take majority votes on ‘p’ and ‘if p then q’ and derive its judgment on ‘q’ from its majority judgments on the first two propositions.¹² In the present example, the truth-value of ‘q’ is not always settled by the truth-values of ‘p’ and ‘if p then q’; so the group may need to strengthen its premises in order to make them sufficient to determine its judgment on the conclusion. Similarly, in the example of the French Constituent Assembly, propositions ‘p’ and ‘q’ might be designated as premises and proposition ‘r’ as a conclusion. The premise-based procedure would then amount to what Elster (2007, pp. 410-411) describes as a hypothetical ‘double aggregation’ procedure, according to which the Assembly would have voted, firstly, on whether stabilizing the regime is desirable (a normative premise) and, secondly, on whether bicameralism is a way to achieve stability (an causal-empirical premise), before deriving its collective judgment on whether or not to introduce bicameralism (the overall conclusion).

Alternatively, if a group assigns priority to the conclusions, it may use the so-called conclusion-based procedure, whereby it takes majority votes only on the conclusions and makes no collective judgments on the premises. This is the procedure that the French Constituent Assembly actually used. In addition to violating systematicity, this aggregation procedure also violates decisiveness, by producing no judgments on the premises. But sometimes the conclusions are the only propositions that matter from a practical perspective, and in such cases the lack of any collective judgments on the premises may be defensible.

The premise- and conclusion-based procedures are not the only aggregation procedures violating systematicity. The group might not only assign priority to the premises, but also assign different such premises to different subgroups, thereby introducing a division of cognitive labour. Under the so-called distributed premise-based procedure, different individuals specialize on different premises and express their individual judgments only on these premises. The group then makes a collective judgment on each premise by taking a majority vote on that premise among the relevant ‘specialists’, and derives its collective judgments on the conclusions from the specialists’ majority judgments on the premises. I will come back to this procedure in my discussion of the correspondence challenge below.

For many cognitive tasks performed by groups, giving up systematicity and using a premise-based or conclusion-based procedure may be an attractive way to avoid the impossibility result explained above. Each of these procedures allows the group to produce consistent collective judgments. In the case of the premise-based procedure (in either the regular or the distributed form), the group further ensures the deductive closure of its judgments. Such a group can be interpreted as a ‘reason-driven’ proto-agent that derives its collective judgments on conclusions from its collective judgments on relevant premises. Pettit (2001) sometimes speaks of the collectivization of reason in this context.

Still, relaxing systematicity has a price. Aggregation procedures that violate it are vulnerable to various types of strategic manipulation. As should be apparent, their outcomes can be potentially manipulated by agenda setters who have control over the choice of premises. Further, such procedures may give individuals incentives to misrepresent their premise-judgments so as to lead the group to adopt conclusion-judgments they prefer (Dietrich and List 2007e). For example, if the French Constituent Assembly had used the premise-based procedure, the outcome under truthful voting would have been the endorsement of bicameralism. For this reason, both the reactionaries on the right and the radicals on the left, who each opposed bicameralism (albeit for different reasons), would have had incentives to strategically misrepresent their opinions on the premises so as to prevent this outcome. The reactionaries would have been able to prevent a bicameralist outcome by expressing an insincere causal-empirical judgment that bicameralism will not stabilize the regime, contrary to their real opinion; and the radicals would have been able to do the same by expressing an insincere normative judgment that stabilizing the regime is not desirable, contrary to their real attitude.

3.5 Lessons to be drawn

I have shown that a group’s capacity to meet the coherence challenge depends on its aggregation procedure: in general, a group can ensure the consistency of its judgments only if it uses a procedure that violates one of universality, decisiveness or systematicity – or if it willing to install a dictatorship (or even more perversely, an inverse dictatorship) of one individual. Moreover, different aggregation procedures may lead to different outputs for the same inputs. As an illustration, Table 5 shows the collective judgments for the individual judgments in Tables 2 and 3 under different aggregation procedures.

Table 5: Different aggregation procedures applied to the individual judgments in Tables 2 and 3

	Expert panel	French Assembly
	‘p’	‘if p then q’	‘q’	‘p’	‘q’	‘r’
Majority voting*	True	True	False	True	True	False
Premise-based procedure with ‘p’, ‘if p then q’ as premises	True	True	True	True	True	True
Conclusion-based procedure with ‘q’ as conclusion	No judgment	No judgment	False	No judgment	No judgment	False
Distributed premise-based procedure with individual 1 specializing on ‘p’ and individual 2 specializing on ‘if p then q’	True	False	False	False	True	False
Unanimity rule	No judgment	No judgment	No judgment	No judgment	No judgment	No judgment
Dictatorship of individual 3	False	True	False	True	False	False

* inconsistent

If we were to use collective coherence as the only criterion of wisdom – disregarding correspondence with any relevant external facts – this would give us insufficient grounds for selecting a unique aggregation procedure. As illustrated, there are many possible procedures that produce consistent collective judgments, and even if we require deductive closure as a criterion of coherence in addition to consistency, several of these procedures remain. It is therefore time to turn to the correspondence challenge. At this point, however, I can safely conclude that, contrary to what the impossibility results on judgment aggregation may seem to suggest, the possibility of collective coherence is not ruled out.

4. Meeting the correspondence challenge

We have seen that there are several routes by which a group can ensure the coherence of its judgments. Can a group also ensure the correspondence of those judgments with the relevant facts? In order to address this question, I must first define the notion of correspondence with the facts more carefully.

Consider some proposition ‘p’, which is factually true or false, such as the proposition that the average particle pollution level exceeds a certain amount in the expert-panel example, or the proposition that the defendant in a criminal trial did a particular action. An agent’s judgment on ‘p’ corresponds with the facts just in case the agent judges that ‘p’ if and only if ‘p’ is true. Since most agents are fallible, however, their judgments correspond with the facts at best approximately. To quantify how well they do, I will consider two conditional probabilities (List 2006b): first, the conditional probability that the agent judges that ‘p’, given that ‘p’ is true; and, second, the conditional probability that the agent does not judge that ‘p’, given that ‘p’ is false. Call these two conditional probabilities the agent’s positive and negative reliability on ‘p’, respectively. In some cases these two probabilities coincide, in others they differ. An agent may be better at identifying the truth of ‘p’ than its falsehood, or the other way round. A doctor performing a diagnostic test on a patient, for example, may be better at detecting the presence of some disease if the patient has the disease than its absence if the patient does not. Or an expert advisory committee may be better at detecting the presence of some risk if there is such a risk than its absence if there is not. To meet the correspondence challenge with respect to a given proposition ‘p’, I will assume, an agent must have a high positive and negative reliability on ‘p’.¹³ A simple illustration shows that one of the two alone is not enough. Consider a medical advisory panel that always judges that a particular chemical is safe – call this proposition ‘p’ – regardless of how dangerous the chemical is. This committee would thus have a positive reliability of one on ‘p’: if the chemical were truly safe, the committee would certainly say so. But it would have a negative reliability of zero: even if the chemical were extremely dangerous, the committee would still deem it safe. The committee’s judgments would not co-vary at all with the truth.

By considering a group’s positive and negative reliability on various propositions under different aggregation procedures and different scenarios, I will now identify conditions under which the group succeeds at meeting the correspondence challenge. It turns out that three principles of designing an aggregation procedure may promote collective wisdom: the principles of democratization, decomposition and decentralization.

4.1 The effects of democratization

Suppose, to begin with, that a group seeks to make a judgment on a single factual proposition, such as the proposition that air pollution is above a particular threshold or that a defendant is guilty. As originally suggested by Condorcet (1785), suppose, further, the group members’ individual judgments on proposition ‘p’ satisfy two favourable conditions:

Competence: Each group member has a positive and negative reliability r above a half, but below one, on proposition ‘p’, so that individuals are fallible in their judgments but biased towards the truth. For simplicity, all individuals have the same reliability, for example r = 0.6.

Independence: The judgments of different group members are mutually independent.

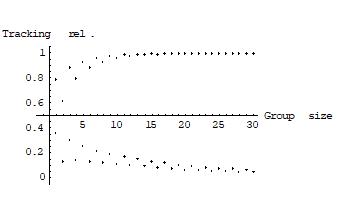
These conditions are highly idealized, and a lot could be said about scenarios in which they are violated¹⁴Indeed, in a recent paper, Franz Dietrich (2008) goes so far as to argue that there are no situations in which Condorcet’s two conditions are simultaneously justified.. What is the group’s positive and negative reliability on ‘p’ under various aggregation procedures? Consider three aggregation procedures: first, as a degenerate baseline case, a dictatorship of one individual, where the group’s judgment on ‘p’ is always determined by the same fixed individual group member; second, the unanimity rule, where agreement among all group members is necessary and sufficient for reaching a collective judgment on ‘p’; and third, majority voting on ‘p’. Figures 1, 2 and 3 show the group’s reliability on ‘p’ under these three aggregation procedures. The group size is plotted on the horizontal axis, the group’s positive and negative reliability on ‘p’ on the vertical one.

Under a dictatorship, the group’s positive and negative reliability on ‘p’ equals that of the dictator, which is 0.6 in the present examples. Here the group performs no better and no worse at meeting the correspondence challenge than any of its members. Unsurprisingly, a dictatorial collective is no wiser than its dictator taken individually.

Figure 1: The group’s positive and negative reliability under a dictatorship

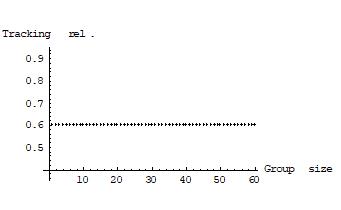
Figure 2: The group’s positive and negative reliability under unanimity rule

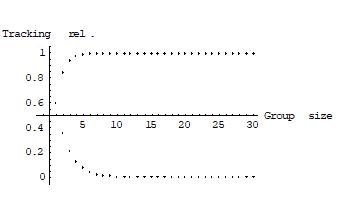
Figure 3: The group’s positive and negative reliability under majority voting

Note: The difference between the reliability for an odd group size (top curve) and an even one (bottom curve) is due to the fact that majority ties are impossible under an odd group size but possible under an even one.

Under the unanimity rule, the group’s positive reliability on ‘p’ approaches zero as the group size increases: it equals rⁿ. In a ten-member group with an individual reliability of 0.6, for example, this is 0.006. But the group’s negative reliability on ‘p’ approaches one as the group size increases: it equals 1-(1-r)ⁿ. In the same example of a ten-member group, this is 0.999. Moreover, a determinate group judgment on ‘p’ – that is, a judgment that ‘p’ or that ‘not p’ – is reached only if all individuals agree on the truth-value of ‘p’. If they do not, no group judgment on ‘p’ is made. In a large group, the unanimity rule is almost certain to produce no group judgment on ‘p’ at all, which makes it rather useless in many judgmental or decision-making tasks. This observation echoes my earlier remarks about the risk of indecision under unanimitarian or supermajoritarian aggregation procedures.

Finally, and most strikingly, under majority voting, the group’s positive and negative reliability on ‘p’ exceeds that of any individual group member and approaches one as the group size increases. This is, of course, Condorcet’s jury theorem.

Why does the theorem hold? By the competence condition, each individual has a probability r above a half of making a correct judgment on ‘p’, and by the independence condition different individuals’ judgments are independent from each other. So each individual’s judgment is like an independent coin toss, where one side of the coin, say heads, corresponds to a correct judgment, which comes up with a probability of r, say 0.6, and the other side, tails, corresponds to an incorrect judgment, which comes up with a probability of 1-r, say 0.4. How often would you expect the coin to come up heads when it is tossed many times? Statistically, given the independence of different tosses, you expect heads in 6 out of 10 cases and tails in 4 out of 10 cases. In the case of just ten tosses, of course, the actual heads-tails pattern may still deviate from the expected one of 6-4: it may be 7-3, or 5-5, or sometimes 4-6. But now consider the case of a hundred tosses. Here the expected heads-tails pattern is 60-40. Again, the actual pattern may deviate from this; it may be 58-42, or 63-37, or 55-45. But it is less likely than in the case of ten tosses that we get heads less often than tails. Now in the case of a thousand, ten thousand, or a million tosses, it is less and less likely, by the law of large numbers, that the coin comes up heads less often than tails, given the expected frequency of 0.6. Translated back into the language of judgments, the probability of a majority of individuals making a correct judgment approaches one as the group size increases, as required by the Condorcet jury theorem.¹⁵ The competence and independence conditions are crucial for this result. If individual reliability falls below 1/2, the mechanism leading to a likely majority of coin tosses on the correct side ceases to apply; in fact, then the probability of a majority of tosses on the wrong side approaches one with increasing group size. Similarly, if different individuals’ judgments are not independent, but instead highly correlated with each other, then aggregating them will not significantly enhance overall reliability. Whether or not majoritarian aggregation is truth-conducive in the presence of less extreme interdependencies between individual judgments depends on the precise nature of these interdependencies (e.g., Boland 1989; Ladha 1992; Dietrich and List 2004; Berend and Sapir 2007).

What lesson can be drawn from this? If group members are independent, fallible, but biased towards the truth in their judgments, majority voting outperforms both dictatorial and unanimity rules in terms of maximizing the group’s positive and negative reliability on a given proposition ‘p’; the only strength of unanimity rule is that it is good at avoiding false positive judgments, but at the expense of many false negative ones. Hence, when a group seeks to meet the correspondence challenge, there may be epistemic gains from democratization, that is, from adopting a majoritarian democratic structure.

4.2 The effects of decomposition

Suppose now a group seeks to make a judgment not just on a single factual proposition, but on an agenda of several interconnected ones (for detailed analyses on which the present discussion draws, see Bovens and Rabinowitz 2003; List 2006b). For example, the group could be a university committee deciding on whether a junior academic should be given tenure, with three relevant propositions involved: first, the candidate is excellent at teaching; second, the candidate is excellent at research; and third, the candidate should be given tenure, where excellence at both teaching and research is necessary and sufficient for tenure. More generally, there are k ≥ 2 premises and a conclusion which is true if and only if all the premises, and thereby their conjunction, are true. Alternatively, the conclusion could be true if and only if at least one premise, and thereby their disjunction, is true; the analysis would be very similar to the one given here for the conjunctive case. The French Constituent Assembly discussed above provides another example of the conjunctive case, though here some complications arise from the fact that one of the premises is a normative proposition which does not, on all accounts, have an independent truth value.

The first thing to note is that, in this case of multiple propositions, individuals do not generally have the same reliability on all propositions. The members of a tenure committee, for example, may be better at making correct judgments on the separate premises about teaching and research than on the overall conclusion about tenure. More generally, if each individual has the same positive and negative reliability r>1/2 on each premise and makes independent judgments on different premises, then his or her positive reliability on the conclusion is r^k, which is below r and can easily be below a half,¹⁶ The latter happens whenever r is below the k^th root of a 1/2. while his or her negative reliability on the conclusion is above r and thus always above a half. Here individuals are worse at detecting the truth of the conclusion than the truth of each premise, but better at detecting the falsehood of the conclusion than the falsehood of each premise. Other scenarios can be constructed, but it remains the case that individuals typically have different levels of reliability on different propositions (for further discussion, see List 2006b). Condorcet’s competence assumption cannot generally be sustained once we are dealing with multiple interconnected propositions.

What is the group’s positive and negative reliability on the various propositions under different aggregation procedures? As before, assume that the group members’ judgments are mutually independent. Majority voting performs well only on those propositions on which individuals have a positive and negative reliability above a half. In other words, majority voting performs well on a given proposition if the individuals satisfy Condorcet’s competence condition on it, assuming they also satisfy the independence condition. But as just argued, individuals may not be sufficiently competent on every proposition. In addition, majority voting may fail to ensure coherent group judgments on interconnected propositions, as already shown. Let me therefore set majority voting aside and compare dictatorial, conclusion-based and premise-based procedures. Again, dictatorships are discussed mainly in order to provide a baseline case for comparison.

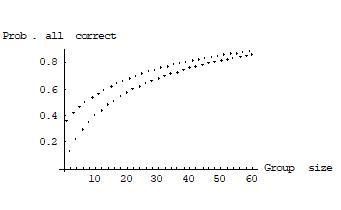
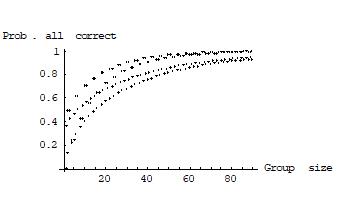
Suppose, as an illustration, there are two premises as in the university committee example and individuals have a positive and negative reliability of 0.6 on each premise and are independent in their judgments across different premises. Figures 4 and 5 show the group’s probability of judging all propositions correctly under a dictatorship and under the premise-based procedure, respectively. Figure 6 shows the group’s positive and negative reliability on the conclusion under the conclusion-based procedure. As in the earlier figures, the group size is plotted on the horizontal axis and the probabilities in question on the vertical one.

Figure 4: The group’s probability of judging all propositions correctly under a dictatorship

Figure 5: The group’s probability of judging all propositions correctly under the premise-based procedure

Note: The difference between the reliability for an odd group size (top curve) and an even one (bottom curve) is due to the fact that majority ties are impossible under an odd group size but possible under an even one.

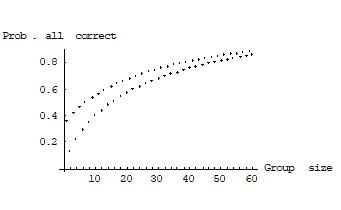
Figure 6: The group’s positive and negative reliability on the conclusion under the conclusion-based procedure

Note: The difference between the reliability for an odd group size (top curves) and an even one (bottom curves) is due to the fact that majority ties are impossible under an odd group size but possible under an even one.

Generally, under a dictatorship of one individual, the group’s positive and negative reliability on each proposition equals that of the dictator. In particular, the probability that all propositions are judged correctly is r^k, which may be very low, especially when the number of premises k is large. Under the conclusion-based procedure, unless individuals have a very high reliability on each premise,¹⁷ To secure this result, each individual’s positive and negative reliability on each premise must exceed the k^th root of a half, e.g., 0.71 when k = 2, or 0.79 when k = 3. the group’s positive reliability on the conclusion approaches zero as the group size increases. Its negative reliability on the conclusion approaches one. Under the premise-based procedure, finally, the group’s positive and negative reliability on every proposition approaches one as the group size increases. This result holds because, by the Condorcet jury theorem, the group’s positive and negative reliability on each premise approaches one with increasing group size, and therefore the probability that the group derives a correct judgment on the conclusion also approaches one with increasing group size.

What lessons can be drawn from this second scenario? Under the assumptions made, the premise-based procedure outperforms both dictatorial and conclusion-based procedures in terms of simultaneously maximizing the group’s positive and negative reliability on every proposition. Again, a dictatorship is bad at pooling the information contained in the judgments of multiple individuals. And the conclusion-based procedure, like the unanimity rule in the single-proposition case, is good at avoiding false positive judgments on the conclusion, but usually bad at reaching true positive ones (Bovens and Rabinowitz 2003). For instance, even if there are only two premises and individual reliability r on each premise is above 1/2 but below the square root of 1/2, for example, r = 0.65, each individual’s probability of detecting the truth of the conclusion, if it is true, is r², which is below 1/2. Thus, by the reverse of Condorcet’s jury theorem, the probability of a correct majority judgment on the conclusion, if it is true, converges to zero as the group size increases.

Hence, if a larger judgmental task such as making a judgment on some conclusion can be decomposed into several smaller ones such as making judgments on certain relevant premises from which the conclusion-judgment can be derived, this decomposition can promote collective wisdom.

4.3 The effects of decentralization

When a group is faced with a complex judgmental task involving several propositions, different group members may have different levels of expertise on different propositions. This is an important characteristic of many collectives, such as expert panels, groups of scientific collaborators, multi-member courts, central banks, firms, organizations, governments, and so on. Even in a group as small as a tenure committee, the representatives of the university’s teaching and learning centre may be better qualified to assess the candidate’s teaching than some of the other committee members, whereas the latter may be better qualified to assess the candidate’s research. Individuals may simply lack the resources to become sufficiently well-informed on every proposition. If we take this problem seriously, can we improve on the premise-based procedure?

Suppose, as before, a group seeks to make collective judgments on an agenda containing k different premises and a conclusion which is true if and only if all the premises are true. Instead of requiring every group member to make a judgment on every premise, the group may subdivide itself into several subgroups, for simplicity of roughly equal size: one for each premise, where the members of each subgroup specialize on their assigned premise and make a judgment on it alone. In the tenure committee example, one subgroup may consist of the teaching assessors and the other of the research assessors. Instead of a using a regular premise-based procedure as in the previous scenario, the group may now use a distributed premise-based procedure, as defined earlier. Here the collective judgment on each premise is made by taking a majority vote within the subgroup specializing on the given premise, and the collective judgment on the conclusion is then derived from the specialists’ majority judgments on the premises.

Can the distributed premise-based procedure outperform the regular one at maximizing the group’s reliability? Two effects pull in opposite directions here. On the one hand, there may be epistemic gains from specialization: individuals may become more reliable on the propositions on which they specialize. But on the other hand, there can also be epistemic losses from lower numbers: each subgroup voting on a particular proposition is smaller than the original group: it is only roughly 1/k of the size of the original group when there are k premises, and this may reduce the information-pooling benefits of majority voting on that proposition.

Whether or not the distributed premise-based procedure outperforms the regular one depends on which of these two effects is stronger. If there were no epistemic gains from specialization, then the distributed premise-based procedure would suffer only from losses from lower numbers on each premise and would thus perform worse than the regular premise-based procedure. On the other hand, if the epistemic losses from lower numbers were relatively small compared to the epistemic gains from specialization, then the distributed premise-based procedure would outperform the regular one.

To give a simple example, suppose there are twenty individuals making judgments on two premises, where each individual’s reliability on each premise is 0.6 without specialization. And suppose further that if we subdivide the group into two halves specializing on one premise each, then each individual’s reliability on the assigned premise goes up to 0.7. At first sight, these gains from specialization seem relatively modest. However, it turns out that the group is better off by opting for the decentralized arrangement and using the distributed premise-based procedure. Each ten-member subgroup with an individual reliability of 0.7 will make a more reliable judgment on its assigned premise than the twenty-member group as a whole with each individual’s reliability at 0.6. In the present numerical example, the original group’s positive and negative reliability on each premise will be 0.7553, while each specialist subgroup will have a reliability of 0.8497 on its assigned premise. The following theorem generalizes this point:

Theorem (List 2005; 2008): For any group size n (divisible by k), there exists an individual reliability level r^* > r such that the following holds. If, by specializing on proposition ‘p’, individuals achieve a positive and negative reliability above r^* on ‘p’, then the majority judgment on ‘p’ in a subgroup of n/k specialists, each with reliability r^* on ‘p’, is more reliable than the majority judgment on ‘p’ in a group of n non-specialists, each with reliability r on ‘p’.

Hence, if by specializing individuals achieve a reliability above r^* on their assigned premise, then the distributed premise-based procedure outperforms the regular one. How great must the reliability increase from r to r^* be in order to have this effect? Surprisingly, a relatively small increase is enough. Table 6 shows some illustrative calculations. For example, when there are two premises, if the original individual reliability in a 50-member group was 0.52, then a reliability above 0.5281 after specialization is sufficient; if it was 0.6, then a reliability above 0.6393 after specialization is enough.

Table 6: Reliability increase from r to r^* required to outweigh the loss from lower numbers

	k = 2, n = 50	k = 3, n = 51	k = 4, n = 52
r	0.52	0.6	0.75	0.52	0.6	0.75	0.52	0.6	0.75
r*	0.5281	0.6393	0.8315	0.5343	0.6682	0.8776	0.5394	0.6915	0.9098

Figure 7 shows the group’s probability of judging all propositions correctly under regular and distributed premise-based procedures, where there are two premises and individuals have positive and negative reliabilities of 0.6 and 0.7 before and after specialization, respectively. Again, the group size is plotted on the horizontal axis, and the relevant probability on the vertical one.

Figure 7: The group’s probability of judging all propositions correctly under the distributed and regular premise-based procedure

Note: The difference between the reliability for an odd group size (top curves) and an even one (bottom curves) is due to the fact that majority ties are impossible under an odd group size but possible under an even one.

The lesson from this third scenario is that, even when there are only relatively modest gains from specialization, the distributed premise-based procedure may outperform the regular one in terms of maximizing the group’s positive and negative reliability on every proposition. Decentralization may therefore promote collective wisdom. If a group seeks to meet the correspondence challenge, it may thus benefit from subdividing its judgmental tasks into several smaller ones and distributing them among multiple subgroups. Plausibly, such division of cognitive labour is the mechanism underlying many of the successes of collective wisdom in science and in suitably structured organizations (Knorr Cetina 1999; Giere 2002; Page 2007).

5. Concluding remarks

I have discussed the lessons we can learn about collective wisdom by combining insights from the emerging theory of judgment aggregation with insights from Condorcet’s jury theorem. I have discussed two dimensions of wisdom – wisdom as coherence and wisdom as correspondence – and I have asked under what conditions a group can attain wisdom on each of these dimensions.

With regard to the achievement of collective coherence, I have discussed an impossibility theorem by which we can characterize the logical space of aggregation procedures that ensure coherent collective judgments. When the propositions on which judgments are to be made are non-trivially interconnected, no non-dictatorial (and non-inverse-dictatorial) aggregation procedure generating consistent collective judgments can simultaneously satisfy universality, decisiveness and systematicity. To find a non-degenerate aggregation procedure that produces coherent collective judgments, then, it is necessary to relax one of these three conditions. Which relaxation is most defensible depends on the group and the cognitive task it is faced with.

With regard to the achievement of collective judgments that accurately correspond to the facts, I have identified three principles of organizational design that can promote collective wisdom: there may be benefits from democratization, from decomposition and from decentralization. The applicability and magnitude of each benefit depends on the group and cognitive task in question, and there may not be a ‘one size fits all’ aggregation procedure that is best for all groups and all cognitive tasks. But the possibility of each of these benefits underlines the potential for collective wisdom.

Overall, the present results paint a fairly optimistic picture of collective wisdom, contrary to the negative picture that the impossibility results on judgment aggregation seem to suggest at first sight. Of course, the details of this picture depend on a number of assumptions and favourable conditions and may change with changes in them. However, possibility results such as the ones discussed here can be illuminating, and I hope to have illustrated the usefulness of the present theoretical approach in identifying the conditions that promote collective wisdom and those that undermine it.

References

Arrow, K. (1951/1963). Social Choice and Individual Values. New York, Wiley.

Berend, D. and L. Sapir (2007). “Monotonicity in Condorcet’s Jury Theorem with Dependent Voters.” Social Choice and Welfare 28(3): 507-528.

Boland, P. J. (1989). “Majority Systems and the Condorcet Jury Theorem.” The Statistician 38: 181-189.

Bovens, L. and W. Rabinowitz (2003). “Complex Collective Decisions: An Epistemic Perspective.” Associations 7: 37-50.

Condorcet, M. d. (1785). Essay sur l’Application de l’Analyse à la Probabilité des Décisions Rendue à la Pluralité des Voix. Paris.

Dennett, D. (1987). The Intentional Stance. Cambridge, Mass., MIT Press.

Dietrich, F. (2006). “Judgment aggregation: (im)possibility theorems.” Journal of Economic Theory 126(1): 286-298.

Dietrich, F. (2007). “A generalised model of judgment aggregation.” Social Choice and Welfare 28(4): 529-565.

Dietrich, F. (2008). “The Premises of Condorcet’s Jury Theorem Are Not Simultaneously Justified.” Episteme: A Journal of Social Epistemology 5(1): 56-73.

Dietrich, F. (forthcoming). “The possibility of judgment aggregation on agendas with subjunctive implications.” Journal of Economic Theory.

Dietrich, F. and C. List (2004). “A Model of Jury Decisions Where All Jurors Have the Same Evidence.” Synthese 142: 175-202.

Dietrich, F. and C. List (2007a). “Arrow’s theorem in judgment aggregation.” Social Choice and Welfare 29(1): 19-33.

Dietrich, F. and C. List (2007b). “Judgment aggregation by quota rules: majority voting generalized.” Journal of Theoretical Politics 19(4).

Dietrich, F. and C. List (2007c). Majority voting on restricted domains. London School of Economics.

Dietrich, F. and C. List (2007d). Opinion pooling on general agendas, London School of Economics.

Dietrich, F. and C. List (2007e). “Strategy-proof judgment aggregation.” Economics and Philosophy 23(3).

Dietrich, F. and C. List (2008). “Judgment aggregation without full rationality.” Social Choice and Welfare 31: 15-39.

Dokow, E. and R. Holzman (2006). Aggregation of binary evaluations with abstentions, Technion Israel Institute of Technology.

Dokow, E. and R. Holzman (forthcoming). “Aggregation of binary evaluations.” Journal of Economic Theory.

Dryzek, J. and C. List (2003). “Social Choice Theory and Deliberative Democracy: A Reconciliation.” British Journal of Political Science 33(1): 1-28.

Elster, J. (2007). Explaining Social Behavior: More Nuts and Bolts for the Social Sciences. Cambridge, Cambridge University Press.

Estlund, D. (1994). “Opinion Leaders, Independence, and Condorcet’s Jury Theorem.” Theory and Decision 36: 131-62.

Gärdenfors, P. (2006). “An Arrow-like theorem for voting with logical consequences.” Economics and Philosophy 22(2): 181-190.

Genest, C. and J. V. Zidek (1986). “Combining Probability Distributions: A Critique and Annotated Bibliography.” Statistical Science 1(1): 113-135.

Giere, R. (2002). “Distributed Cognition in Epistemic Cultures.” Philosophy of Science 69: 637-644.

Goldman, A. (2004). “Group Knowledge versus Group Rationality: Two Approaches to Social Epistemology.” Episteme: A Journal of Social Epistemology 1(1): 11-22.

Goodin, R. E. and C. List (2006). “Special Majorities Rationalized.” British Journal of Political Science 36(2): 213-241.

Grofman, B., G. Owen, et al. (1983). “Thirteen theorems in search of the truth.” Theory and Decision 15: 261-278.

Guilbaud, G. T. (1966). Theories of the General Interest, and the Logical Problem of Aggregation. Readings in Mathematical Social Science. P. F. Lazarsfeld and N. W. Henry. Cambridge, Mass., MIT Press: 262-307.

Knight, J. and J. Johnson (1994). “Aggregation and Deliberation: On the Possibility of Democratic Legitimacy.” Political Theory 22(2): 277-296.

Knorr Cetina, K. (1999). Epistemic Cultures: How the Sciences Make Knowledge. Cambridge, MA, Harvard University Press.

Kornhauser, L. A. and L. G. Sager (1986). “Unpacking the Court.” Yale Law Journal 82.

Kornhauser, L. A. and L. G. Sager (1993). “The One and the Many: Adjudication in Collegial Courts.” California Law Review 81: 1-59.

Ladha, K. (1992). “The Condorcet Jury Theorem, Free Speech and Correlated Votes.” American Journal of Political Science 36: 617-634.

Lehrer, K. and C. Wagner (1981). Rational Consensus in Science and Society. Dordrecht/Boston, Reidel.

List, C. (2001). Mission Impossible: The Problem of Democratic Aggregation in the Face of Arrow’s Theorem. Politics. Oxford, Oxford University.

List, C. (2003). “A Possibility Theorem on Aggregation over Multiple Interconnected Propositions.” Mathematical Social Sciences 45(1): 1-13 (with correction in Math Soc Sci 52, 2006: 109-10).

List, C. (2004). “A Model of Path-Dependence in Decisions over Multiple Propositions.” American Political Science Review 98(3): 495-513.

List, C. (2005). “Group knowledge and group rationality: a judgment aggregation perspective.” Episteme: A Journal of Social Epistemology 2(1): 25-38.

List, C. (2006a). The Democratic Trilemma. Democracy and Human Values Lectures, Princeton University. Princeton/NJ.

List, C. (2006b). “The Discursive Dilemma and Public Reason.” Ethics 116(2): 362-402.

List, C. (2008). Distributed Cognition: A Perspective from Social Choice Theory. Scientific Competition: Theory and Policy, Conferences on New Political Economy vol. 24. M. Albert, D. Schmidtchen and S. Voigt. Tuebingen, Mohr Siebeck.

List, C. (forthcoming). Judgment aggregation: a short introduction. Handbook of the Philosophy of Economics. U. Mäki. Amsterdam, Elsevier.

List, C. and R. E. Goodin (2001). “Epistemic Democracy: Generalizing the Condorcet Jury Theorem.” Journal of Political Philosophy 9: 277-306.

List, C., R. C. Luskin, et al. (2000/2006). Deliberation, Single-Peakedness, and the Possibility of Meaningful Democracy: Evidence from Deliberative Polls. London School of Economics. London, London School of Economics.

List, C. and P. Pettit (2002). “Aggregating Sets of Judgments: An Impossibility Result.” Economics and Philosophy 18: 89-110.

List, C. and P. Pettit (2004). “Aggregating Sets of Judgments: Two Impossibility Results Compared.” Synthese 140: 207-35.

List, C. and P. Pettit (forthcoming). Group agency: The Possibility, Design and Status of Corporate Agents.

List, C. and C. Puppe (forthcoming). Judgment aggregation: a survey. Oxford Handbook of Rational and Social Choice. P. Anand, C. Puppe and P. Pattanaik. Oxford, Oxford University Press.

Miller, D. (1992). “Deliberative Democracy and Social Choice.” Political Studies 40(special issue): 54-67.

Nehring, K. and C. Puppe (2002). Strategyproof Social Choice on Single-Peaked Domains: Possibility, Impossibility and the Space Between. University of California, Davis, University of California, Davis.

Nehring, K. and C. Puppe (2002/2007). Abstract Arrovian Aggregation, University of Karlsruhe.

Page, S. E. (2007). The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies. Princeton, Princeton University Press.

Pauly, M. and M. van Hees (2006). “Logical constraints on judgement aggregation.” Journal of Philosophical Logic 35: 569-585.

Pettit, P. (1993). The Common Mind: An Essay on Psychology, Society and Politics, paperback edition 1996,. New York, Oxford University Press.

Pettit, P. (2001). “Deliberative Democracy and the Discursive Dilemma.” Philosophical Issues (supp to Nous) 11: 268-99.

Pigozzi, G. (2006). “Belief merging and the discursive dilemma: an argument-based account to paradoxes of judgment aggregation.” Synthese 152: 285-298.

Rubinstein, A. and P. Fishburn (1986). “Algebraic Aggregation Theory.” Journal of Economic Theory 38: 63-77.

Surowiecki, J. (2004). The Wisdom of Crowds: Why the Many Are Smarter Than the Few. London, Abacus.

Wilson, R. (1975). “On the Theory of Aggregation.” Journal of Economic Theory 10 89-99.